Link to: Home page for map making related material
Measuring the un-measurable.. and making a map
Fun(?) activity with some mathematics?
Mathematics which are a little fun, too?
file: mapCT.htm
I first started "playing" with the ideas and techniques here when I was about 12. I've had a lot of fun with related things over the years. It didn't seem "fun" at first, but it amazes me how the strangest things can "grow on you", if you make the effort to get past the "foothills" of the learning curve.
There are a lot of words here. To the people for whom this was written: Please do not be put off. It is a very do-able activity. If you are now be a long way from Haddam, you can still do this. ("You can do this, Billy..."). When you've at least skimmed the page you are reading, there is a page with the numbers you could have collected when you were at Haddam. (That will open in a new window or tab... If your browser isn't set to switch to that, don't think that the link didn't work!)
Anyway, all of what follows can be done in many places. I would love to hear from anyone how "has a go", either with the Haddam situation, or with a comparable location elsewhere. If you are lucky, and live in a place with views from hilltops, you can map across amazing distances. (Your map can be accurate, but scale-less. Or, you can allow yourself one "cheat"... use the work of other people to find how far apart your "Alice" and "Bob" places are (see below). See also: How they found out how high Everest is... without even going TO Everest. In 1856. No GPS. No cell phones. No motor vehicles... well... apart from steam engine driven trains. And they didn't run very far into the Himalayas!)
To teachers, youth group leaders, etc: I was a teacher of 8-13 year olds for many years. If I could have a chance to talk with you, I believe I could convince you that it would "work"... either as "educational", or for a "free time" activity. Yes, you will have to figure out what I have tried to say, "re-package" it to suit the group you want to deliver it to. But there is "good stuff" here, that can give you a flying start.
By a happy coincidence of where sundry things are, just below the Haddam bridge, on the Connecticut River, there's a place where the width of a 750' wide river can be figured out by kids from one bank of the river...
...with not much more than a pizza box, some paper, Scotch tape, an 18" bit of wood with two nails in it, a small table, or small step ladder, a tape measure and a compass (of the "draw a circle" type). Remarkable accuracy is also possible.
Yes! this page speaks very specifically about taking these first steps towards a map in a particular place. If you have just a little imagination, I trust you can see how it can be adapted to some similar place near you?

History and purpose of this page: Written for a specific group, 9/19, but it is also a "new improved" work, put on the internet for anyone who wants to use the ideas. Part of an ever-growing body of work.
My apologies to any who find the "narrative" style of the opening discussion annoying. Some readers would have found a more formal description too reminiscent of schooldays they would rather forget: "Given: A triangle, ABC. In any triangle, the sum of the angles is 180, i.e. BAC + ACB + CBA will always be 180." Ehh??
Imagine Alice and Bob on a long dock by a wide river. The river runs from the north the south. The long axis of the dock runs parallel to the riverbank. (We'll get to how a group could have fun doing this in due course.)
The dock isn't essential to the exercise. The same thing can be done from places on a level grassy bit beside a river... but there are special advantages to using the dock, if you have one.
Imagine that they wonder "How wide is the river?"
"How wide is the river?" is easily answered! Well.. the "work" is minimal. Why that minimal work tells you how wide the river is takes a bit of... shudder... thinking. And the easy "work" has to be done carefully. (Practicing thinking and practicing working carefully are not bad ways to spend your time, you know.)
The answer is in two parts:
- Alice and Bob will need to gather three numbers
- They'll need to draw a diagram
In addition to those two sections, this webpage has sections for more detail about..
- How to capture the angles easily and accurately.
- How to transfer an angle drawn in one place to an angle of the same size in another.
- How the surveyor can see if the answer obtained is correct.
- How this activity can be made fun for groups.
First step... gathering the numbers...

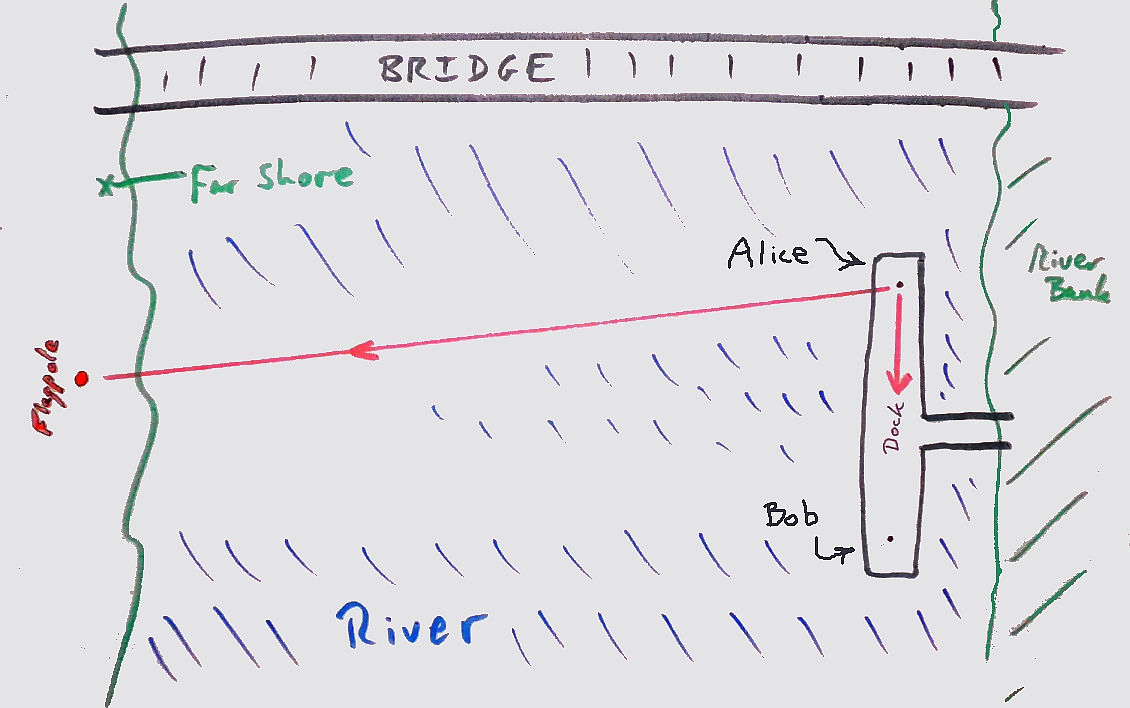
Alice and Bob, on the dock
(or shore) on the east side of the river, pick a spot on the west shore of the river. A flagpole, perhaps.
(Remember: If you are no longer able to go to the dock shown, the numbers you could have collected when you were at Haddam are availble to you. I have put the answer *I* got to "how wide is the river there too. (And you can use the techniques set out here in many, many places. If you do the exercise someplace else, I would love to hear about it.)
That page also gives you the answers I got to "how wide is the river"... two different answers, one for each of the ways you can copy the angles from the plane table records to your map. My best answer is near the bottom of that page.
Keeping their eyes on that spot, they go to opposite ends of the dock. Alice goes to the north end, Bob to the south end.
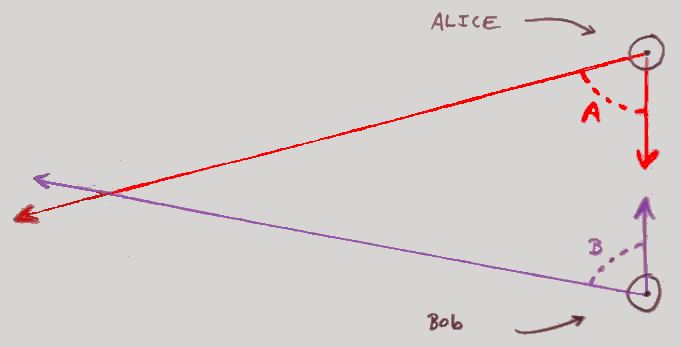
Alice points her left arm at Bob, and her right arm at the flagpole. Then she measures the angle between her arms, as seen from over her head. (We'll come back to this; it isn't as hard as it might seem.) Let's say it comes to 79 degrees.
V V
V V
("Arms, Debbie"?)
Obviously, just pointing arms won't give an accurate measure of the angle. The "pointing arms" is just to get you started. How the angles are measured, easily and accurately, is explained later.
------------
First Alice, north end of dock, points arms, and measures the angle between her arms, as seen from over her head....
----------------
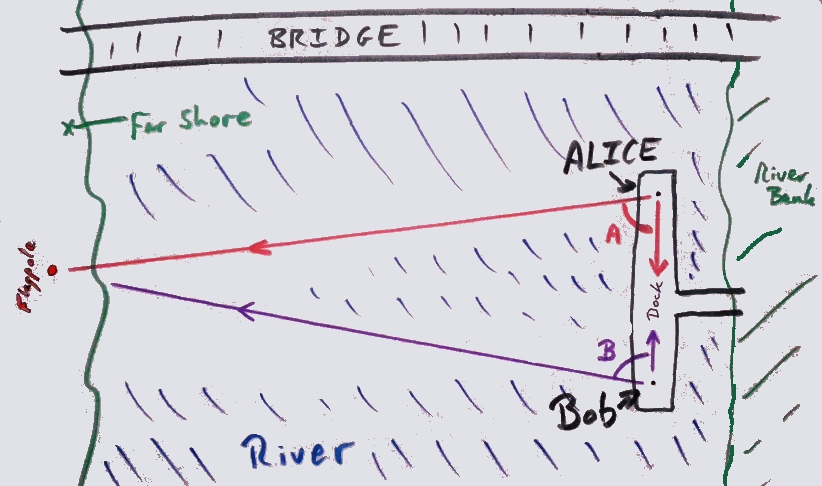
Now Bob repeats the exercise from his end of the deck.
Bob points his right arm at Alice, and his left arm at the flagpole. Then he measures the angle between his arms. Let's say it comes to 70 degrees.
Then they measure how far apart they were when they did this. Let's say it comes to 130 feet, as it would, if the dock was 150 feet long, like the one at Haddam, but they were each 10 feet from their end of the dock when they determined the angles.
They now have everything they need to figure out how far they were from the flagpole!
Using the numbers- drawing the diagram...
So- two angles, and a distance.
For this explanation, let's say the river wasn't very wide... about 300 feet, maybe? The angles given above are about right for a 300 foot wide river. (Using 300 feet allows diagrams that fit on this page better.) The river at Haddam is about 750 feet wide.
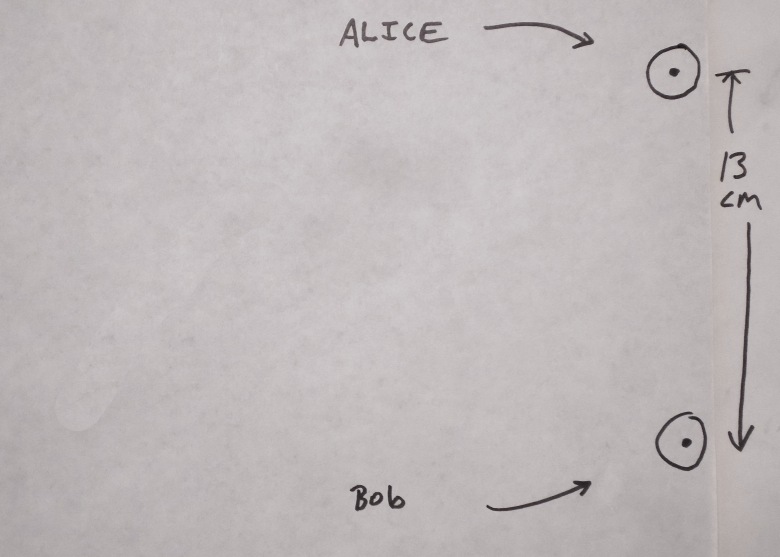
Alice and Bob take a sheet of paper, and put two dots on it. Theoretically, they could be "anywhere"... but if the dots are in the "wrong" places Alice and Bob would end up having to stick extra bits of paper to the first to finish the challenge.
For whatever reason, they put their dots on the right hand side of a sheet oriented in landscape mode. And they put them 13 cm apart. They choose 13 cm because they were 130 feet apart on the dock.
On the map 1 cm represents 10 feet because they have used 13 cm. (Forgive the mixing of unit systems?)
(Even the separation of the dots on the page can be anything you like. It only changes the scale of the map.)
Where's "North"? The dock runs more or less North/South. Alice was at the North end. Thus, with the dots as described, North is roughly at the top of the diagram we are building. Getting the rotation exactly right for "North at the top" is easily done, and I will try to get to describing that later.
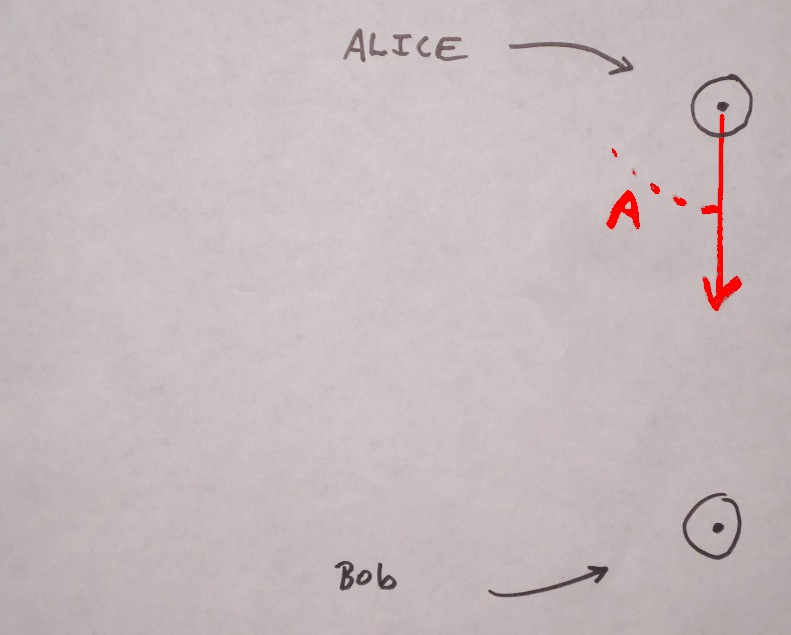
Then they draw in the angles.
Remember: Alice was at the north end of the dock. Her angle was 79 degrees. The line from her left hand HAS to go where shown, because that's where Bob was. The other line goes where ever it must, to give the correct angle.
Then they repeat the exercise to draw Bob's angle (They make his angle 70 degrees on the diagram, with one arm pointing to Alice. The same way they drew her angle onto the diagram.) Resulting in....
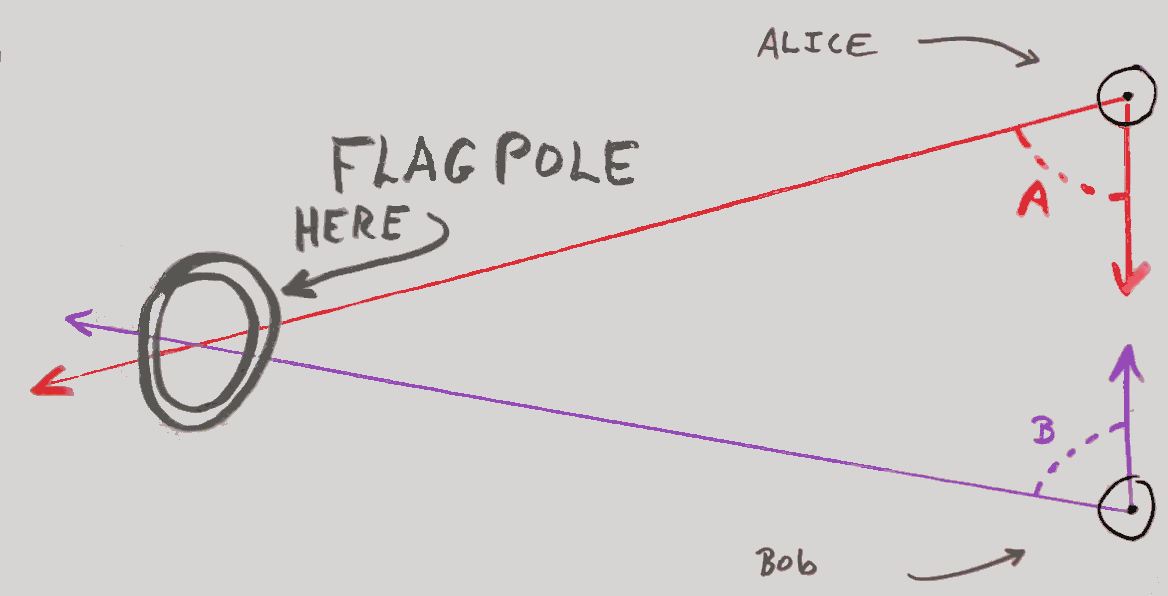
Where the lines from Alice and Bob CROSS is where what they were pointing to is on the diagram! They have made a start on a "map". It isn't a very useful map yet, showing only the two ends of a dock and a flagpole....
... but "all" they would have to do to make their map more useful would be to add more points to it.
For instance: The locations of the west end and middle of the big bridge just north of the dock could be added by exactly the same technique.
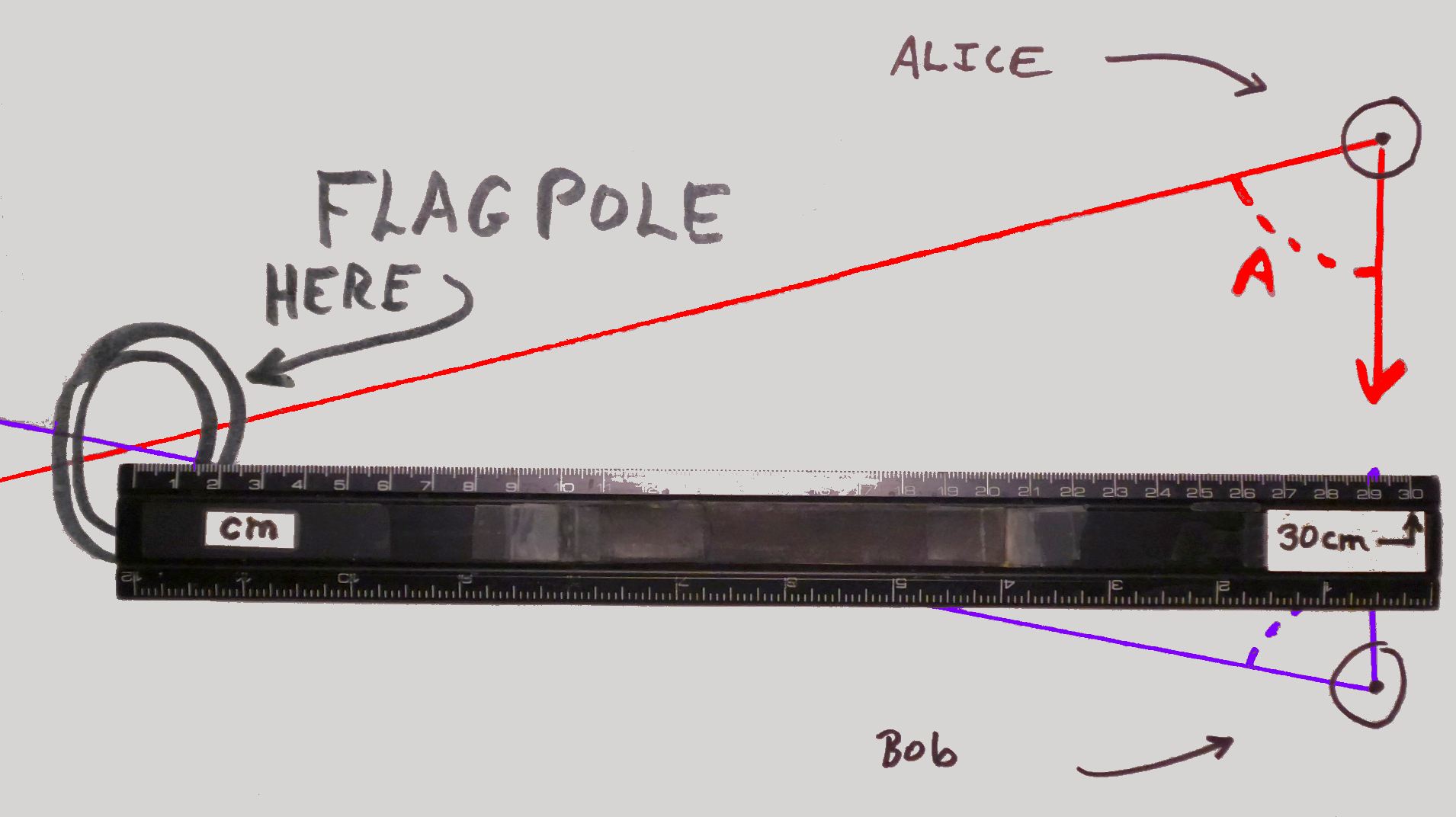
As the place where the lines cross is 29 cm from the dock on our diagram, that flagpole (not the one at Haddam where the angles would have been different) is 290 feet from the dock. (Our map was drawn using 1cm for 10 feet, remember? The dot's for Alice and Bob are 13 cm apart because they were 130 feet apart.)
Real maps, until not long before the British miner's strike of 1984, were based on this system of map making. Even today, an element of this approach remains in map making, and maps are made more often than you might think. (For instance, when land is bought and sold, the exact boundaries are very interesting the to parties concerned)
PLEASE NOTE....
The diagrams here were done with fat nibbed markers, to make them easy to read. I hope you will be using sharp pencils, with "hard" lead, or a good drawing pen, like a 0.5mm "Pilot Precise" Rollerball or similar. The sharp pencil or good pen will give you a better result.
How to capture the angles easily and accurately
Alice and Bob could have gone to an antiques store, and bought a beautiful instrument called a theodolite.
Or, they might use....
- A pizza box
- A step ladder
- A bit of wood with two nails in it.
- A tape measure (to see how far apart Alice and Bob were)
There's an expensive answer to every problem. But if you think... then there's often another answer.
I'm not just making all of this up as I go along. I've actually done the exercise, with, literally, a pizza box. I would guess that the answer I got was probably correct within no more than 50 feet... across a 750 foot river, without going anywhere except on the dock.
Here's what I used to measure the angles.It is an inexpensive... but still effective, "plane table" (The one
I used was even simpler than the "deluxe" model shown on the linked page.)

(If have a small, easily moved, solid (not wobbly) table, it would probably be better than the step ladder which was all I had.)
The pizza box was taped down, so it wouldn't move. A large sheet of paper was taped to it.
The thing that is lying on the box is a bit of wood with a straight edge, and two nails sticking up. (Picture below, right.).
The user lines up the nails on something, and draws a line along the bit of wood, onto the paper. The ruler/sight is then lined up on a new target, a new line is drawn, and thus the angle is captured.
This (photo) is the "tool" for pointing at something, and making a line on the piece of paper on the plane table. The black sticky up things at the ends are the two nails. They serve as "sights". (I could supply several to the people this was initially written for.)

If you decide to actually try this, have a look at a page about a detail about where to draw the lines when using the plane table.
How to transfer an angle drawn in one place to an angle of the same size in another
You "capture" (measure from "life") the angles with a plane table, which leaves you with lines on a piece of paper, but no number, yet.
You could just use a protractor to measure the angle. And then you would use it again, to make the right sized angle on your diagram.
But do you need to know the angle, in degrees? No! And, if you proceed as follows, you don't need to know the size of the angle in degrees, either. So we'll be having no protractors, thank you very much. And with a decent sized compass, you can probably copy the angle from the plane table "data collection document" to the final diagram more accurately, anyway.
See separate page about copying angles with a drawing compass.
How the surveyor can see if the answer obtained is correct.
To the east of the dock this example is built around, there is a picnic area.
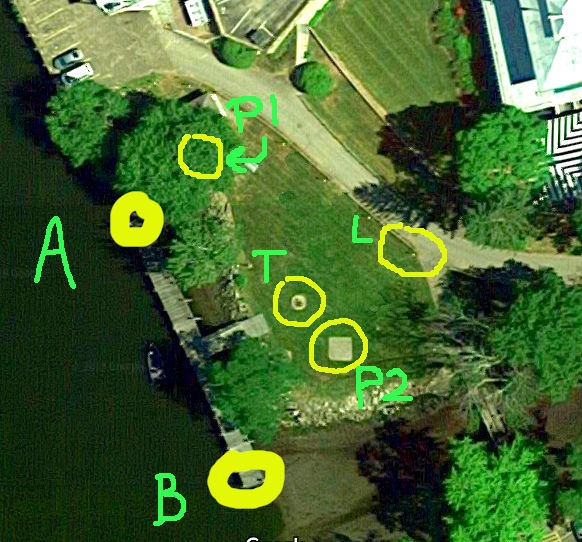
That's a bit scruffy... will try to improve.
The image above shows the dock running between where Alice was (Bold yellow circle, labelled "A"), and where Bob was, B.
Roughly clockwise from A, we have...
- P1: north picnic table
- L: The lamp by path on 8' post that I suggest as "trial run" target.
- P2: south picnic table
- T: The top of a Tank, set into the ground.
Start with locating "L" on your diagram (stick paper to the side, as needed).
THEN GO TO "L", "point one arm" at "A", and the other at "B".
On your diagram, draw a line as close as you can from L to A.
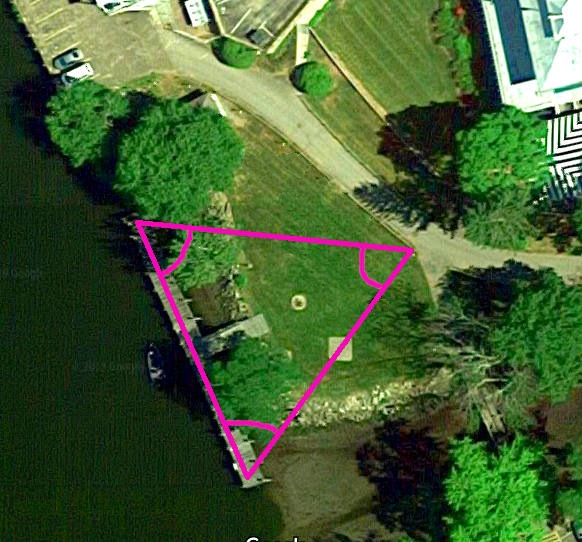
Now, with the apex at L, draw the angle you measured, i.e. draw ALB. That line SHOULD pass through the dot you made at the start of all this, for B. If it does, that "proves" that you measured all three angles correctly. If it is slightly off, then one or more of your angles is off... and it could be any of them.
THIS IS HOW YOU CHECK THAT you've "got it right".
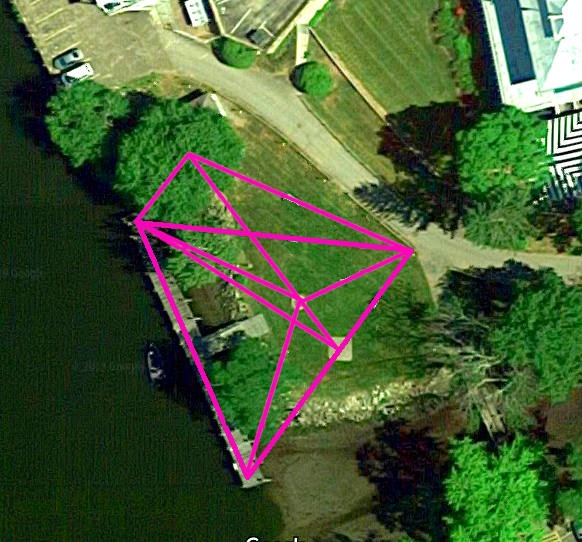
And for the really keen, you repeat the exercise from all of the other "stations"- from the two picnic tables, from the tank. (A specific PLACE on the tank.)
(Unimportant digression... another!)
Look closely at the cover of the tank.
You will find the following. It is a few inches across...

That was set in the concrete to "mark a spot", "forever", by earlier mappers working here.
With "marked spots" like that, they can come back to gather new data, check old, etc.
The "original" "main spots" for THE map of England were originally marked by wooden posts.
The people in charge soon realized that this would be a poor answer, and replaced them with 16 foot cannons, buried muzzle up with only 2'showing above ground. They are there to this day. Don't stub your toe on one of them... it will not move.
How this activity can be made fun for groups
The "fun"... well, for some people... comes from two things...
Just DOING it at all... measuring the width of the river, without crossing it, DOES amuse some people. I hope you know some people that can get enjoyment from such things.
A bigger category of humans gets pleasure from doing something, anything, WELL. (The group for whom this was written seem to have an admirable commitment to that "do it WELL" attitude.)
If the exercise is done just as described above, two plane tables, one for each end of the dock, or similar positions on the shore, can be shared, turn and turn about. But waiting your turn is BORING. And time is a precious commodity.
(The dock locations have various advantages... not least the fact that the length of the dock has been measured. It is 150 feet, within a few inches, end to end. Put the plane tables in the middle of the "cross" made by imagining lines between the four posts at each of the dock's ends. Remember to measure and allow for not being at the ends of the dock. (The measurement came out "exactly" 150 feet... but my tape was very slightly stretchy. It was a good tape, but it would have had to have been very good (expensive) to have no stretch in 80 feet. All of these things are "lessons" for "science", "mathematics"... life! But you can pretend they are ice cream, not vegetables. The pill has nice sugar around the nasty "good for you" stuff inside.)
But if the group set out to do as much as possible of the following, it only requires a few more tables... the picnic benches will suffice for two of them. And now "teams" (or individuals) can "rotate" between the siting locations. To Alice and Bob's locations at the ends of the dock, we've added more.
At the end of it all, it can be fun to compare the different "answers" people got for how wide the river was, and to look at each other's webs of lines from doing the land based targets.
In fact, BEFORE measuring the width of the river, the ultimate goal, I would have the participants measure the distance from the dock to the light-on-a-post to the East of the dock, as a practice run. Being closer, small errors in measuring the angles, or drawing them, matter less.
I hope it will have occured to you that you don't need to stop at the flagpole? The more points in the real world you measure angles to, from "Alice" and "Bob", the more things you can draw in on your diagram. You will have a map, if you draw in enough. At Haddam, the west end of the bridge, and the middle are obvious candidates.
For W.E. Esq and friends, I can supply suitable paper, and the "sticks with nails in them" for sighting along. And, with a little warning, compasses and maybe protractors. Happy to meet with facilitator of the activity, to run through the practicalities. I do not need to be there on the day... don't worry that I imagine that I will be. Willing, if schedules work, but not "expecting".
Haddam: I wouldn't use the flagpole that is across the river. There are two, easily confused. And if the flag isn't up, it is hard to find. I'd suggest the south end of the top of the roof of the nearer steel shed....

Oh, and another thing... where's North?
Maps usually have an arrow on them showing what direction is North. North is usually at the top of a map.
If you wanted such a line on your map, the easy thing to do is to bring a "find- North" compass (as opposed to "draw- circle" compass with you when you do the field work. If you know what direction your baseline (the Alice/Bob line in the exercise above), then if you are careful about where you put the Alice and Bob dots on your piece of paper at the start of drawing the map, then north will be at the top.
I forgot to bring a compass, when I did the fieldwork for this essay. But I found a way around that lack.
I have been enjoying map making for years...
I first started wondering "How can this be done...?" about 1968. I was working on creating maps by triangulation in 1980. The page above is merely the latest (at 2020) effort to lead others into this wor;d which has fascinated me for so long, and which I believe is very do-able at many different "age-appropriate" levels.
I have to apologise for the poor "overall" organization of the material I have created for you, but if the page above was even mildly interesting, if even "bits" made sense, may I invite you to have a look at my home page for map making related material, which presents similar and related material. Perhaps reading "the same" stuff, presented differently, will help you make sense of what I was trying to convey?
How to email or write this page's editor, Tom Boyd Please mention "SheGui/hh/mapCt.htm" if you do write.
 Page tested for compliance with INDUSTRY (not MS-only) standards, using the free, publicly accessible validator at validator.w3.org. Mostly passes.
Page tested for compliance with INDUSTRY (not MS-only) standards, using the free, publicly accessible validator at validator.w3.org. Mostly passes.
...and passes...

....... P a g e . . . E n d s .....
















