This page throws down a challenge: Can you write the program I need?.. in Lazarus, for my wants... but you could have fun with the challenge for your own purposes in most languages. It all arises out of my Map Making challenges for schools, youth groups, "team building" exercise organizers.
There's not a lot of programming to achieve the first stage of completing the challenge... but there's some tedious mathematics to grasp. I will help you with the mathematics.
You can download the sourcecode of the shell of the program. (Note that there's also a link to a "finished" version, near the bottom of the page.)
Get the first challenge achieved, and then the "real fun" begins! More on that later.
Here's the first challenge...
Suppose I give you the coordinates of three points on a surface....
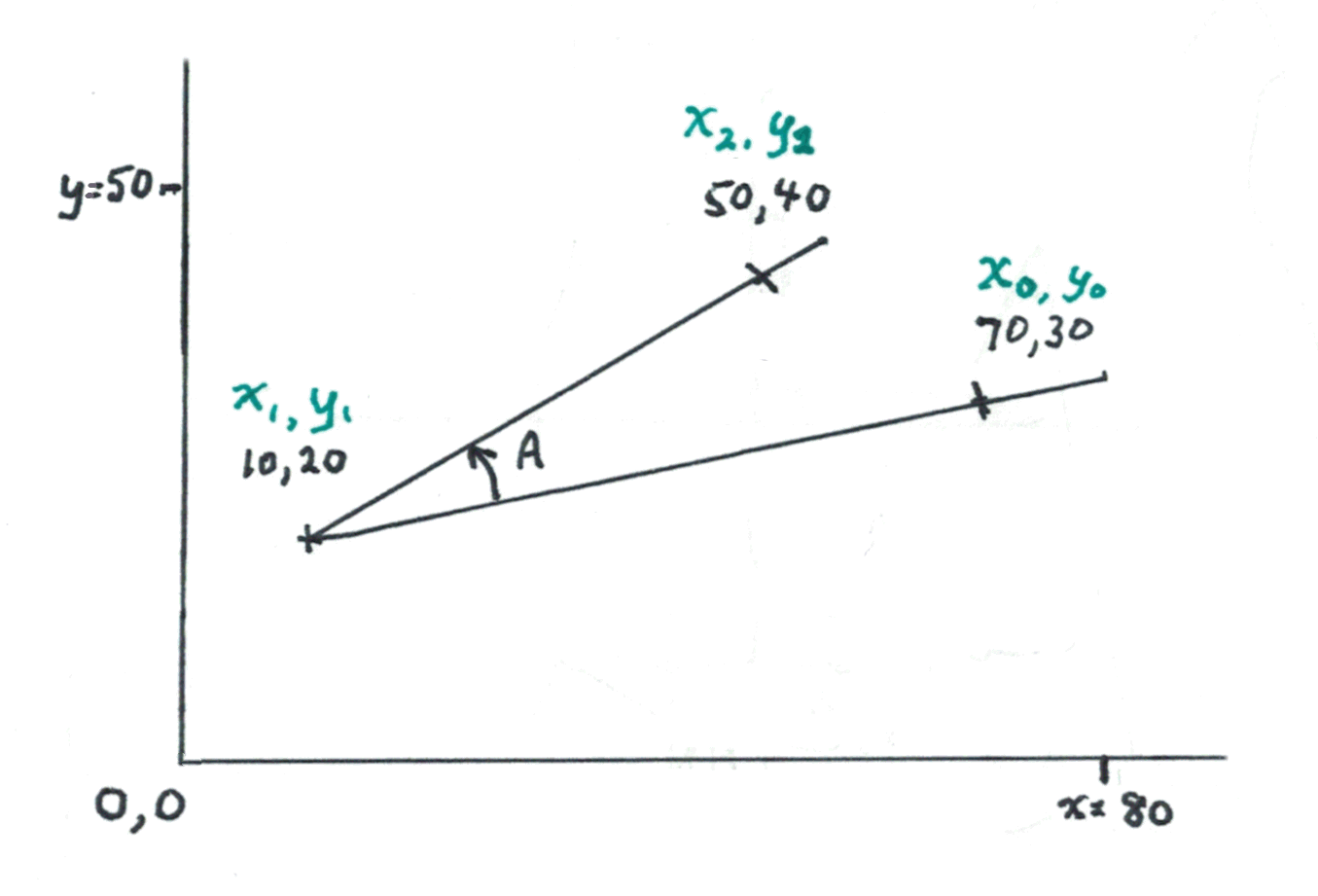
If you draw lines, as above, three points define an angle.
The challenge? Write a subroutine to calculate the angle from the coordinates of the points.
It isn't as hard as it seems. Especially if I promise several things. (I know the following will look "hard", but just take it slowly with an "I CAN do this" attitude! It ISN'T actually hard....)
Why do those things matter? For now, just trust me? (We'll talk about it again, much later, when I change the rules for the second part of the challenge... when things become much harder!)
The first part of the challenge is just to create a little application which will look like this when you run it...
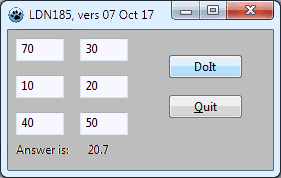
The six numbers (70, 30, 10, 20, 40 and 30) are the coordinates of the three points. They go in edit boxes. (Or, if you would rather, a small text file.. but if you use that method, and read the text file as part of the DoIt handler, copy the 6 values to the screen, so it looks like the screenshot anyway.)
The screenshot (from a mock up of the application that you are challenged to create) shows what the window should look like AFTER the "Do It" button has been clicked.
(The answer, by the way is almost certainly NOT 20.7 !! That is only approximately right! (It was put into the image with a kludge before I knew the exact answer.))
So! You know what the screen should look like.
A bit about the structure of the code that I require of you... "getting the right answer" is NOT enough... it also needs to be done the right way!
Here's a sketch of the OnClick handler for the button captioned "Do It"....
procedure TLDN185f1.buDoItClick(Sender: TObject);
var rAns:real;
x0,y0,x1,y1,x2,y2:integer;
begin
//(fill x0, y0, x1, etc with the values you
// want to do the calculation for)
rAns:=rAngleFromCoords(x0,y0,x1,y1,x2,y2);
laAns.caption:=floattostr(rAns);
end;
If, as would make sense, you use edit boxes as the way the user will tell the application the values of the coordinates, you run the risk that a user will enter something other than text. It is not necessary to deal with that in any depth in attempting the challenge. Maybe just set a flag, and have laAns.caption show "invalid input" unless the flag is clear.
Here's what the subroutine looks like at the moment...
function TLDN185f1.rAngleFromCoords(x0,y0,x1,y1,x2,y2:integer):real; begin result:=20.7; end;
Yes! The program has two x0's, two y0's, etc.
I don't see this as being a problem. The provisions for scope in the language take care of the "problem". In the program this is needed for, when you are working at a "high" level, you won't know what variable names are used inside the sub-routine you will be using. And when you are working on the sub-routine's code, you won't be thinking about what variable hold those values in the "outside" program. Ah, the joys of block oriented programming!
See if you can write the code for the subroutine!
KEEP the elements present in the "sketch" above, e.g. the variable names and what part of the application was broken out into the subroutine.
Use the same variables, and variable types, in the definition of the subroutine.
Please!
I hope the following hints will be enough that you can see what has to be done? By all means write, ask, if bits are unclear.

Here, to save you scrolling, is "the problem" again. And, just to remind you: You have to work out how big the angle ("A") is. In degrees, please. (Not radians... if you've heard of them?)
The first part of working out the size of the angle is to "slide" the angle down and left, until the apex is on the 0,0 point of the Cartesian plane. (For those who know: The "proper" name for what I am speaking about is "translate", not "slide". For those who aren't sure what I mean, look at the diagram. The red angle is the result of sliding/ translating the one we started with to where it needs to be... with the apex at 0,0)
You don't have to provide any graphics for the application. This "sliding down" happens only "inside" the application.
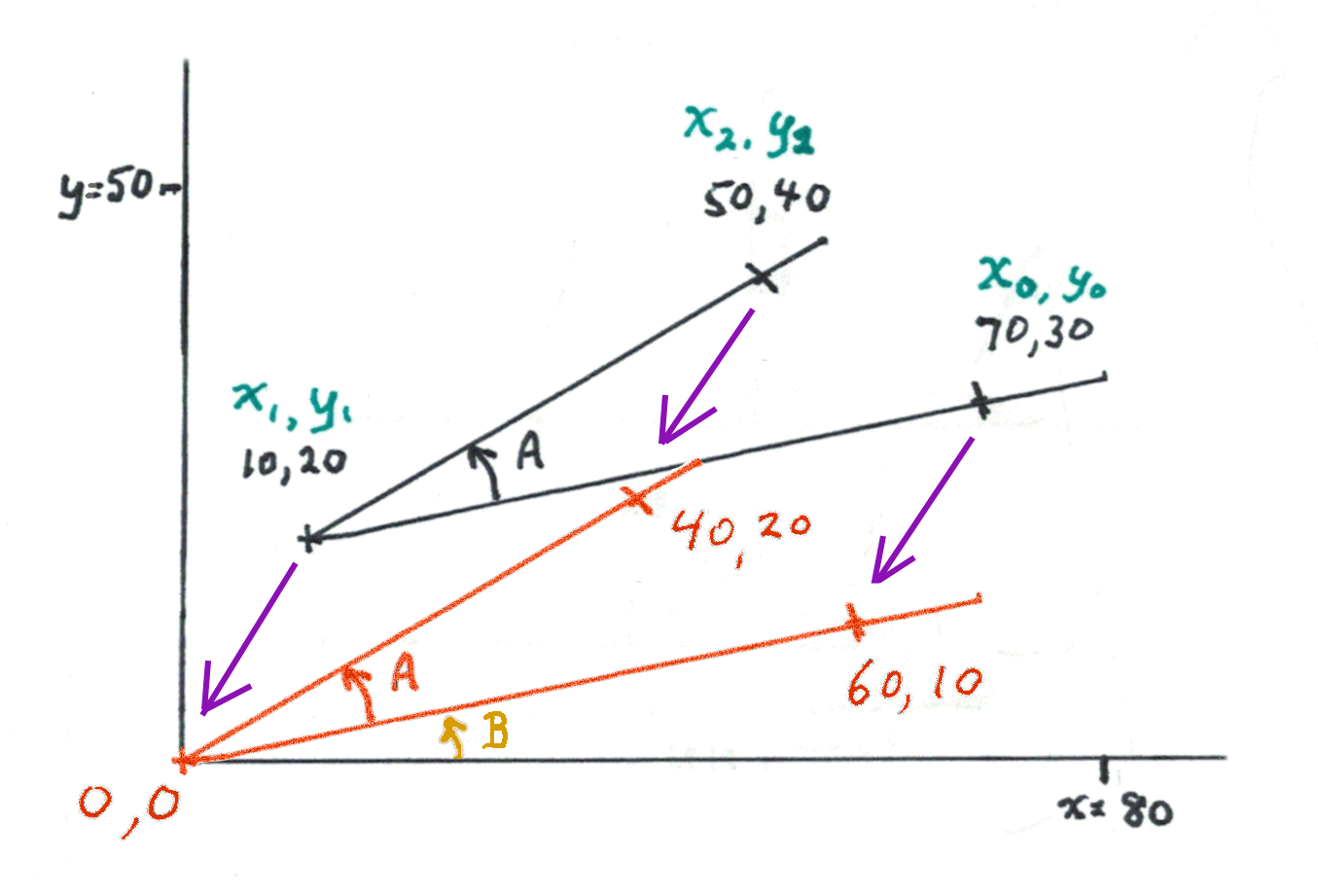
We translate the angle by subtracting one constant number from all three of the x coordinates, and a possibly (but not always) different second constant number from all of the y coordinates. Check the numbers in the diagram. Be sure you are "on the same page" as I'm on.) (Don't worry about angle B yet.)
If we "clean that up" a bit, it is easy to see the angle we wanted to know about. And there's another angle, "B".
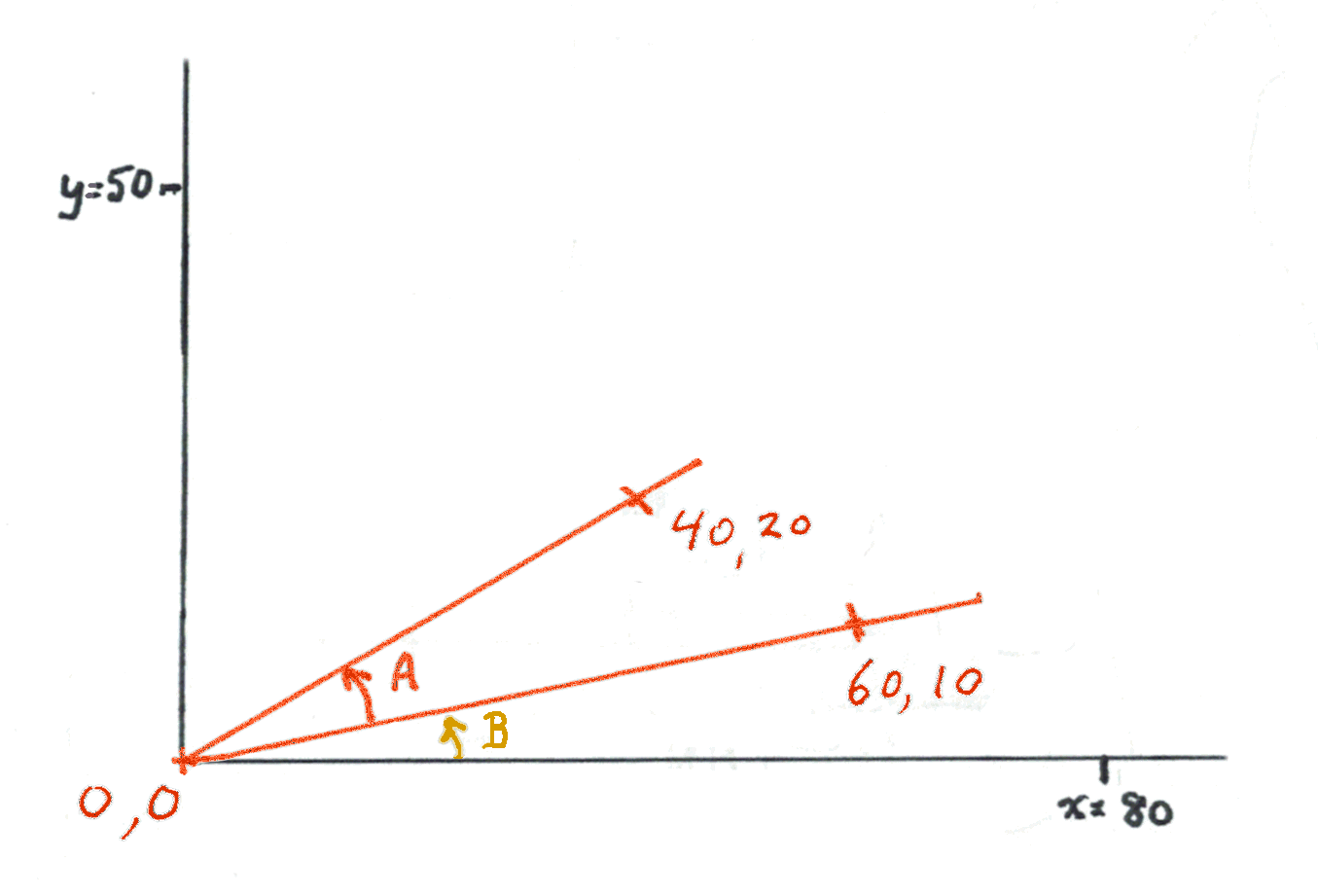
We can figure out what angle A and B make together... let's say it is 35 degrees. And we can figure out how big angle B is. Let's say it is 15 degrees. If we knew those things, we'd know that angle A is 20 degrees!
With trigonometry! Which you won't need to (fully) understand to achieve the challenge. (I may need to write the trig up more than this... but I'm hoping not! As a math teacher to help?)
A digression: I am, in a moment, going to speak of the "arctan" function. That's the function that tells you the angle, if your tell it what the length of the opposite side divided by the adjacent side comes to. E.g. If the opposite side is 5 units long, and the adjacent side is 5 units long, then opposite divided by adjacent comes to 1, and, after you convert the answer from radian to decrees, the arctan of 1 is 45 degrees. It is also called the inverse function of tan, or "cotan". (Thank you, https://www.mathsisfun.com/algebra/trig-finding-angle-right-triangle.html, for reminding me of the details!)
In trig terms, from our diagram, we know the "opposite" and "adjacent" sides of a right triangle: 40,20 / 0,0 / 40,0. (That last point isn't marked on the diagram. You see where it goes, though, don't you? And you see the right triangle? And you see that the adjacent side is 40 units long, and the opposite side is 20 units long? Hurrah! cotan(Opposite/Adjacent), i.e. arctan(20/40), arctan(0.5) will give us the size of the angle made up of "B" and "A" together... 26.56 degrees.
Applying the same logic, arctan(10/60) gives us the size of "B"... 9.46 degrees.
So.. "B" alone is 17.10 degrees!
"All" you have to do is to turn the sliding, the calculation of the two angles (in degrees), and the subtraction of the two... and you'll be done... with the first part of the challenge!
Hint: RadToDeg and arctan are two Lazarus functions which will be useful in this task...
RadToDeg(arctan(Opposite/Adjacent));
("ArcTan()" returns the answer in radians. RadToDeg converts them to degrees. To use RadToDeg, you have to add "Math" to the list of units the application uses.... just add it to the "USES" list at the top of your code.)
My fulsome thanks to the kind reader who submitted a very nice solution.
Before you rush off, and look at the answer... are you sure you don't want to attempt the challenge for your own amusement (and benefit) first? It should take about 20 minutes... and if it doesn't, Making It Work will strengthen your coding skills, so that the next one DOES take only 20 minutes. (Remember: There's a "shell" already prepared for you, downloadable from the link near the top of this page.)
I zipped up the sourcecode submitted, with a copy of the exe for you, and put it online, so you can download it. (The filename will be LTN8chall-angles19222.zip)
His solution is neat and clean. It takes only accepts integers for the coordinate specifications... which is fine. If his solution is extended to solving the second challenge, restricting things to integers probably costs nothing in the use intended for the result. (You can measure the points in the gym in millimeters, if you think it matters.) And it makes the code more efficient... always a worthy goal. Okay. With 200 data points and a modern computer, perhaps we get the result in 0.9 seconds instead of 2.7, but it still a worthy goal!
At the heart of his program....
function rAngleFromCoords(x0,y0,x1,y1,x2,y2: integer): real;
var A1, A2 : real;
begin
A1 := arctan((y2-y1)/(x2-x1));
A2 := arctan((y0-y1)/(x0-x1));
result := RadToDeg(A1-A2);
end;
That's it. That gives you the angle from just the coordinates of the apex, and a point on either side.
Math(s) can be beautiful! If you have the soul to see it.
There were things in what I promised for the three coordinates which made part 1 of the challenge "easy".
Part two of the challenge withdraws some of those promises. The basic technique will still be the same. The code will (mostly) be the same... in fact, changes should ONLY be made within the function definition...
function TLDN185f1.rAngleFromCoords(x0,y0,x1,y1,x2,y2:integer):real; begin result:=20.7; end;
Please don't be "shy"... successes with "only" part 1 of the challenge would be of interest. If you help me with "camera ready" material, I would be glad to showcase what you have done, here.
Please understand: Part (only part) of the reason for creating this page was to get someone else to do the programming for me. (Just doing it myself would have been much less work than doing this page!)... I will assume that you are "giving away ALL your rights" to any code you submit for celebration here. I might well publish it. I, and others, may produce derivative works, and will point to this, if you ask for any payment. I will give you credit, on some level, if I use your stuff. I can't promise that others will.
BEWARE: The search above only visits a selection of my stuff. Go to either of my other sites (see links below) and use that site's FreeFind search button, if you haven't found something you "know is there".
In addition to the tutorials for which this page serves as Table of Contents, I have other sites with material you might find useful.....
My other sites....
Sheepdog Software homepage.
My Arunet homepage.
... and some links to specific pages within them you might want....
You can't "play" all day... learn to use the Libre Office/ Open Office database. Free. Multi-platform.
The Arduino- LOTS of fun, for not much money. And beginner (intelligent beginner) friendly. And good pursuit for kids. Combine programming and electronics!
Designing printed circuit boards the KiCad way. Free. Multi-platform. Long established. PCB-fab houses take native KiCad files.
And lastly... Making maps... how we did it before GPS Indulge me? This discusses a worthwhile, fun (if presented intelligently) activity for kids, which can be undertaken on many levels... a simple 20 minutes, or weeks of engaging activity. (Also known to divert susceptible adults.)
Here is the way to contact the author of these Lazarus/Delphi tutorials, Tom Boyd.
![]() Page has been tested for compliance with INDUSTRY (not MS-only) standards, using the free, publicly accessible validator at validator.w3.org. Mostly passes.
Page has been tested for compliance with INDUSTRY (not MS-only) standards, using the free, publicly accessible validator at validator.w3.org. Mostly passes.
If this page causes a script to run, why? Because of things like Google panels, and the code for the search button. Why do I mention scripts? Be sure you know all you need to about spyware.
....... P a g e . . . E n d s .....