HOME - - - - - - - TUTORIALS INDEX - - - - - - - - - - - - Other material for programmers

Lazarus /Delphi: Using the computer to solve Sudoku puzzles, with some information about using arrays arising along the way

filename: Dt3q,htm

Introduction: Why this material was put onto the web

I don't think you really want to use the application presented in this tutorial to solve Sudokus. The problem of "How could a computer solve a Sudoku?" tempted me, though, so I wrote the program. You might find the way I used an array instructive. That's why I am publishing this.

I don't propose to go into details of what Sudokus are here. Wikipedia has a good article, if you want it.

As a programmer, the following was important to me...

Solving a Sudoku entails filling digits from the set 1..9 into squares. (Zero is not used). Sudokus can be solved by a process of elimination. Look for what can't be in a given cell, and, eventually, you will find cells where 8 of the 9 possibilities have been eliminated. When you fill in the remaining digit as the answer in that cell, what is not possible in other cells is extended. Re-assess the grid, fill in newly discovered digits. Repeat until done.

For an excellent implementation of the game for Android devices, search out the one by Cool Mango.

For more on the theory and practice of Sudoku, see Sabu M H's interesting page. If you download the .zip file and don't read the readme.txt, you may wonder where the .exe file is. It is there... but it was renamed sudoku.bin before being included in the .zip. Just change then name back to sudoku.exe to use it. It worked well, and has a useful option: If you wish, it will flag entries which just can't be right, based on what you know and have guessed so far. It doesn't show you things that are wrong, but, from what you have so far, what could be right. In other words, it protects you from silly mistakes, but won't "give away" the answer. It will also complete the grid of candidate digits for you, if you find that part of the solving process a bit tedious. (There is no way... yet... that I could find... to note candidates "by hand".. in Sabu's version. Tools for that are one of the great strengths of the Cool Mango version.)

I once thought that there were puzzles which could not be solved using just an automatic candidate finder. I now doubt that... I now suspect that any Sudoku can be solved by a program, if your solver's programming is strong enough.

Sometime automatic solvers can only get you to the point were there are only a few... but more than one... candidates fro a particular cell. At that point, you can "play the odds"... or get a better program!

With the Sabu program, to start a new puzzle, either use the button for that, or the "New Puzzle" option under the "Puzzle" menu item. This is only logical, after all, but maybe you, like me, are used to looking for "New..." under the "File" item? Which is about as logical as clicking the "Start" button to stop Windows. The things we can be trained to find "normal"! Sigh.)

What is on the web

A zip file awaits your downloading pleasure. It contains the old version of my sourcecode for most of my Sudoku application. That version does not incorporate all of the things I discuss in this essay.

a) Apologies: I mis-spelt "Sudoku" while working on the project.

b) It was written for Delphi. That should "move" to Lazarus without too much trouble.

c) A critical piece of the heart of the program is incomplete! This is to give you a programming challenge. Have fun. (More is explained below.)

The application, as supplied, will "run" (once compiled), but it will get the answer wrong. It will fill in things where they don't belong, because it will come to wrong conclusions about what can't go in certain places. However, most, if not all, of what you have to re-program is within the UpdateCellInfo procedure.

Stop press, February 2019

The code on offer could be the start of a really good Sudoku solver!

I hope to get back to working on it one day. In the meantime, guidance for those who feel like playing with it...

1) Convert it to Lazarus

2) Be careful to keep the following clear in your mind: The array bInfo is 3x3x10. The first two indices tell you which cell you are dealing with. The last is a bit arcane... If the value in bInfo(x,y,0] is not zero, it tells you what value goes in that cell. If it is zero, then the values in bInfo[x,y,1] to bInfo[x,y,9] will be zeros or 1's. A zero, say in bInfo[x,y,7], means that we haven't yet determined that cell(x,y) can't hold a 7. A 1 in bInfo[x,y,7], on the other hand, says that, if our programming is correct, cell(x,y) cannot hold a 7.

There are many ways to get your gray cells all tangled up when reflecting upon the matters I've just touched on. I would suggest using lots of well named subroutines to manipulate the array.

In February 2019, I revisited this project...

At that time, I thought again, from scratch, about how I would go about the task of programming a computer to solve a Sudoku. This is what I came up with. I suspect that the code presented in the .zip file could easily be brought round to doing the following, in the main "solve it" (or whatever it is called) loop...

REPEAT
  Scan all cells...
     For any where the possibilities have been
     narrowed to just one, "fill that one in".
  Scan all cells...
     For unsolved cells...
        See if any possible answers can be
           ruled out by "rule 0". Mark it
           "not possible" in any such cases.
     For unsolved cells...
        See if any possible answers can be
           ruled out by "rule 1". Mark it.
     For unsolved cells...
        See if any possible answers can be
           ruled out by "rule 2". Mark it.
     ... etc, for as many rules as you can devise.
     (Example of "a rule": Has it already been
        determined that this "possible answer"
        is THE answer for another cell in this row?)
UNTIL SOLVED

The three obvious "that one isn't possible" rules are pretty obvious...

Has that number already been found to be the answer to another cell in this row?

Has that number already been found to be the answer to another cell in this column?

Has that number already been found to be the answer to another cell in this block of 3x3 cells?

... but those aren't the only rules you can apply!

When you've done the loop a few times, most cells will have had their number of "candidate answer" diminished.

If in a given row, column, or 3x3 box of cells, there is only one cell where, say, 6 is a possible answer... then that cell's answer must be 6... even if there are still other "not known to be impossible" answers for that cell. This of course, depends upon you first finding all the answers that are not yet known to be impossible. In doing by hand, this is a pain. In doing it by computer, you start from a "no answer is, as far as we know so far impossible". But the algorithm given weeds the list of not-impossible candidates. (The concept behind this approach may not be easy to grasp... and it will be even more "fun" to program. But it is a sound approach, if you can grasp the idea! In playing the game "by hand", I have yet to find one that cannot be solved with the rules... including this last one... set out above.

End of "Stop press, February 2019"

What the finished application does

When you run the application, a Sudoku puzzle appears on the screen.

There's a button marked "Execute one pass...". Click this, and the application looks at the digits already placed on the screen, and, in each empty cell, marks what digits could not go in that cell. It conveys this information with a a grid of 9 dots (3 rows of 3). If there's a dot in the upper left, then the cell cannot hold a 1. If there's a dot in the upper middle position, then the cell cannot hold a 2, and so on.

If any cell could not hold 8 digits, based on the digits already filled in, then the cell is filled in with the remaining, only possible, digit. (Zeros are not included in Sudoku squares.)

Well... that's what the finished application does. The version supplied in the zip has a fatally stupid UpdateCellInfo procedure. More on that later.

Watching the finished program at work is quite amusing... you see the "can't be that one" dots proliferating with each click of the "Execute one pass...." button.

Structure of the application's code

If I do say so myself, the program is quite well broken down into functional units.

The FormCreate event handler is simply....

begin
FillVarWithDefaults;
FillInKnown;
PrepareDrawingArea;
DisplayTable;
end;

FillVarWithDefaults fills sundry variables with values which will always be good initial values.

FillInKnown fills in values which make the application solve the particular puzzle that it does solve. This is the place you'll have to do some work if you want to extend the application so that it can solve other Sudokus. When you've read the material below about the arrays used in the application, I think you'll understand what is needed.

PrepareDrawingArea is called just once. It sets up an area for plotting "graphics" on. Some text (the filled in digits) is also "plotted" on the canvas, using Lazarus /Delphi's TextOut method.

DisplayTable fills the display with what is known at any given time, digits for known digits, and patterns of dots for digits which cannot appear in a particular cell. It could be improved- the dots remain and make the display a little messy even after the digit for a cell has been deduced. DisplayTable, unlike the other procedures called by FormCreate, is called again, many times, later in the application's execution.

Array used in the application

The "secret" of this application is the array bCellInfo. It is a three dimensional array. Each element holds a byte. Each element of the array will only ever hold a number in the range 0-9, inclusive.

The first two indexes (is that the right term?) tell you which cell in the Sudoku puzzle you are dealing with. e.g., the upper left hand cell's bCellInfo data is held in....

bInfo[0,0,0]
bInfo[0,0,1]
bInfo[0,0,2]
bInfo[0,0,3]
bInfo[0,0,4]
bInfo[0,0,5]
bInfo[0,0,6]
bInfo[0,0,7]
bInfo[0,0,8]... and...
bInfo[0,0,9]

If we have not solved what digit should appear in this cell of the puzzle, then bInfo[0,0,0] will hold 0. Once we have solved the cell, bInfo[0,0,0] holds the number which should appear in the cell. If you look at what is happening during the FillInKnown procedure, you should be reassured that you have understood what I've said so far.

Likewise, if we know that the cell in the bottom left of the puzzle should be filled in with a 5, we will find that bCellInfo[8,8,0] is holding a 5. If the cell in the lower left of the puzzle should be a 9, then bCellInfo[0,8,0] holds a 9.

The other array elements assigned to each cell of the puzzle will all start with 0's in them. Whenever the application determines that a particular cell can't hold a particular digit, one array element is change to hold a 1. E.g.: Suppose we don't yet know what should be in the upper left hand corner of the puzzle, but we deduce that it can't be a 7. We would set bCellInfo[0,0,7] to 1 to record that information.

UpdateCellInfo Revisited

Now that you know a little bit more about the application and its data structure, I can say more about UpDateCellInfo.

The UpDateCellInfo procedure merely calls three sub-routines: UpdateCellInfoHoriz, UpdateCellInfoVert, and UpdateCellInfoLocal8.

The routines look to see what digits are not possible in a particular cell, based on what digits have already been filled in elsewhere. Each routine is called with two parameters. They tell the routine which cell we are working with. E.g., if we are checking what digits are impossible in the center cell of the top row, we call UpdateCellInfo(4,0). Each makes changes to what's in bCellInfo[x,y,d] as appropriate. Other parts of the program, already finished and working, I believe, act on the information.

UpdateCellInfoHoriz looks to see what cells to left and right of the current cell can tell us.

UpdateCellInfoVert looks to see what cells above and below the current cell can tell us.

UpdateCellInfoLocal8 looks to see what cells in the current cell's ninth of the whole puzzle can tell us.

If you've struggled with the programming, and are frustrated and desperate, feel free to email me, and I can send you "the answer"... but please keep it to yourself, to preserve the next person's "fun"?

What's the rule for...

Some of the rules for "this cell holds", or "this cell can't hold" are pretty obvious.

This is a poor photo from the excellent Android "Sudoku Fun" from Cool Mango. At least the old version I have is excellent. Let me know if you experience excessive in-game ads with a later version.

In the image, the big digits are "solved" cells (And the digit IS the right one for that cell, Cool Mango doesn't let you make a wrong move (but records the error if you try to make one.. the idea is to finish the puzzle quickly and with no errors!)).

The little digits are things that COULD go in that cell... but there's no guarantee that you've found ALL that could go in every cell. Although by this point in this game, I think I had.)

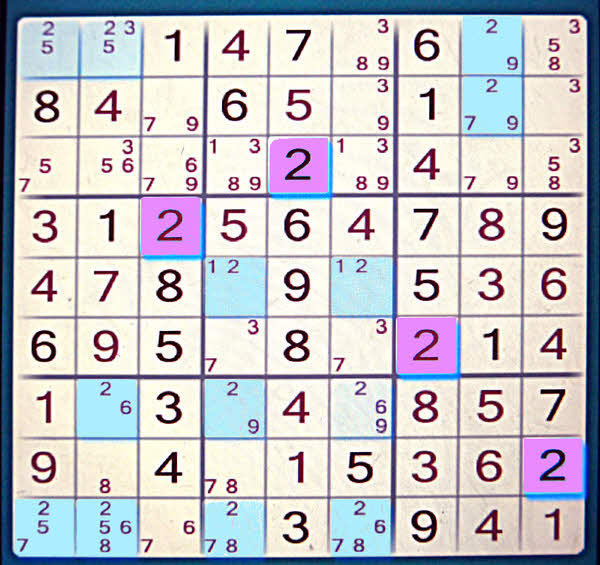
What can you see in the following? (You can say, with certainty, what should go in one of the cells.)

And how would you write the code to search a matrix for things matching the rule you applied?

Highlight...

It is a 2 in the cell one in, and 1 down from the upper right hand corner. (Just to the right of the one that is already solved as a "1". But how do I know? (^_^)

... to here to make answer appear!

And how did I know?

Spoiler Alert!!

Do not scroll down until you have given up trying to figure it out four yourself!

So... here's how you know that a 2 goes in that cell....

-----
Start at the upper left. We know that the 2 for that 3x3 sub-square will be in either the first or the second cell of the top row. Because...

The already placed- in- the- upper- left 3x3 square 8 and 4... plus the two nearest 2s that we already have... prevent us from putting the 2 for the upper left 3x3 anywhere else.

The following trys to say that diagramatically...

________________________________________________
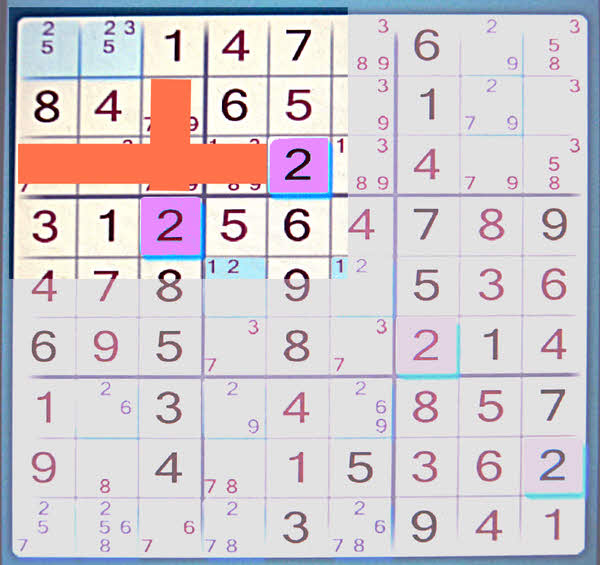
Now, below, look at the upper right hand 3x3 square.

By the same "easy" rules that told us the possible cells for the 2 in the upper left hand square, we can see that the only possible cells for the 2 in the upper right hand square are the ones shown.

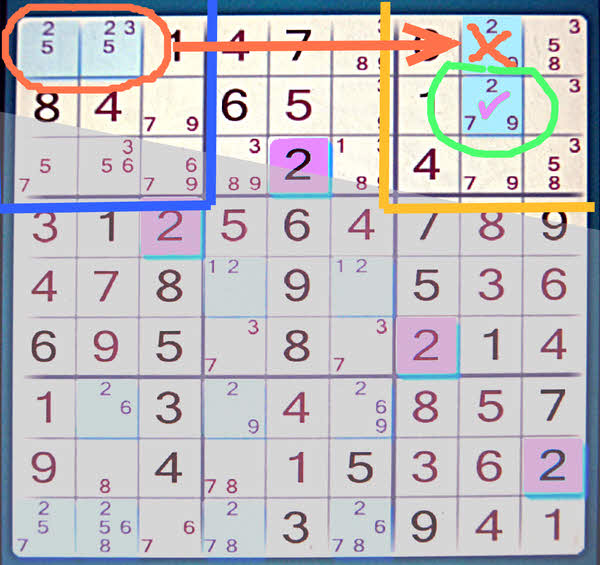
But! Only one of those is possible if you factor in the following additional consideration.

We don't yet know whether the 2 for the upper left 3x3 is in the first or second column... but we know it will be in the top row...

So, since there's a 2 in the top row on the left, there can't be one in the top row in the upper right 3x3 square, can there?!

From our other work, that only leaves the cell in the center of the 3x3 square. Job done! (For the 2.)

As I said: Have fun putting that bit of logic into your Sudoku solving computer program!

Bonus! The colors, to help you with the left and right of things, were inspired by Oliver Byre's 1847 explanation of Euclid's rules for geometry.

Final remarks...

I found the exercise quite fun. I think it would make an excellent challenge for anyone running a programming competition.

Prizes could be offered for various categories:

--Smallest program. (Please stipulate that all variable names must be 8 characters long, to ensure participants use meaningful names!)
--Fastest program. (Time to solve 5 previously unseen Sudokus to determine winner.
--Program successful with fewest variables. (Be careful that no "cheating" is possible, e.g. using the caption of a label to hold data.)

If setting up a competition, an organizer would be wise to stipulate a common data structure for the datafile defining each puzzle, and a standard mechanism for timing how fast the application solves a given puzzle.

Site Map What's New Search

Search across all my sites with the Google search...

Custom Search

Ad from page's editor: Yes.. I do enjoy compiling these things for you... hope they are helpful. However.. this doesn't pay my bills!!! If you find this stuff useful, (and you run a Windows PC) please visit my freeware and shareware page, download something, and circulate it for me? Links on your page to this page would also be appreciated!

Click here to visit editor's Sheepdog Software (tm) freeware, shareware pages.

Link to Tutorials main page

How to email or write this page's editor, Tom Boyd

Page has been tested for compliance with INDUSTRY (not MS-only) standards, using the free, publicly accessible validator at validator.w3.org. Mostly passes.

AND passes...

If this page causes a script to run, why? Because of things like Google panels, and the code for the search button. Why do I mention scripts? Be sure you know all you need to about spyware.

....... P a g e . . . E n d s .....